[Interview] Graph

그래프

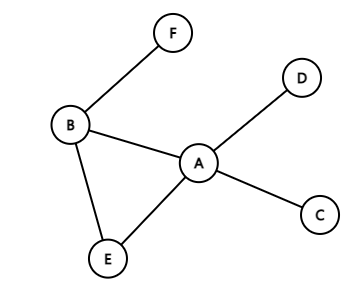
그래프(Graph)란?

• 여러 개의 노드와 그 노드들을 연결하는 간선의 집합으로 구성된 자료 구조

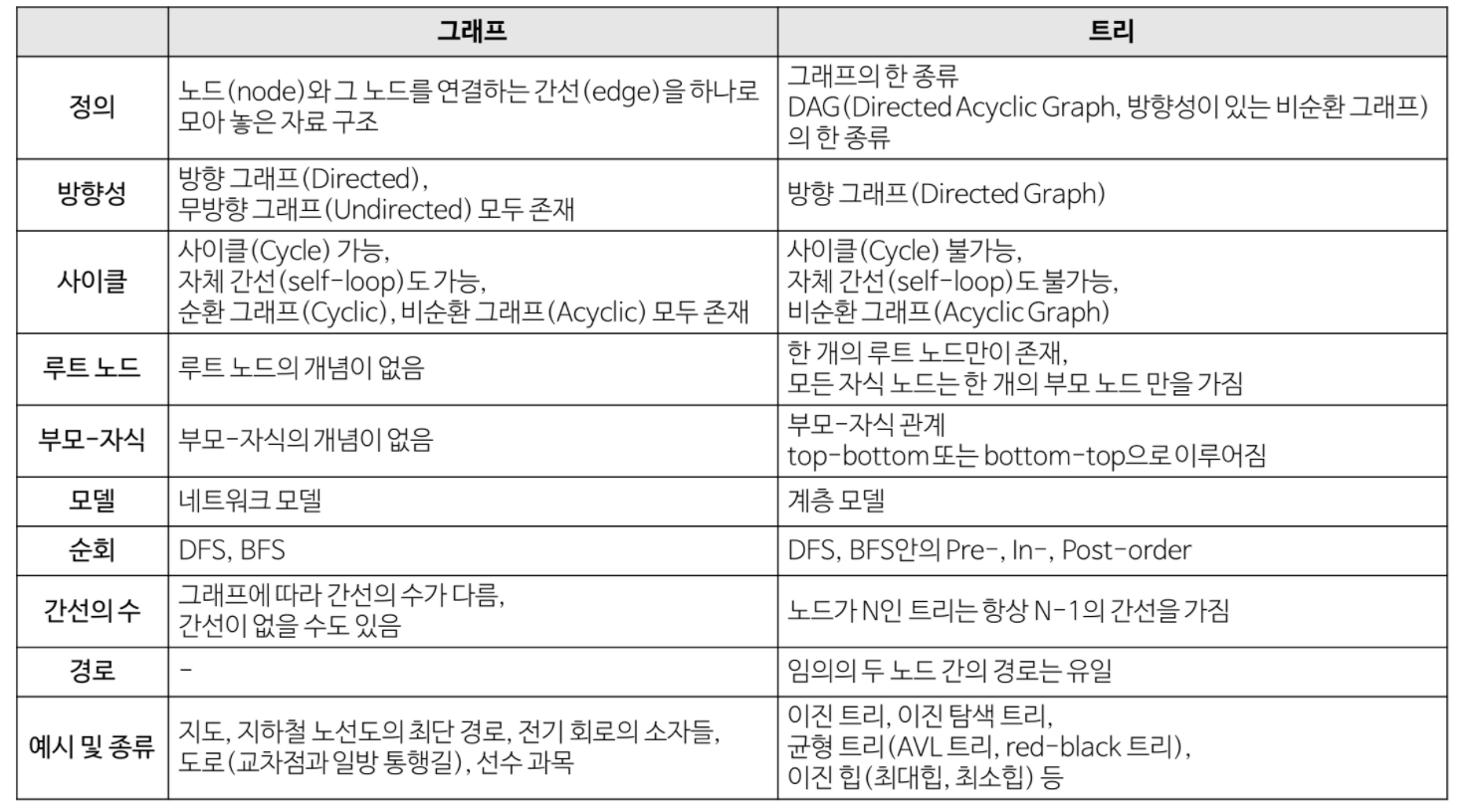
그래프와 트리의 차이점

그래프의 종류

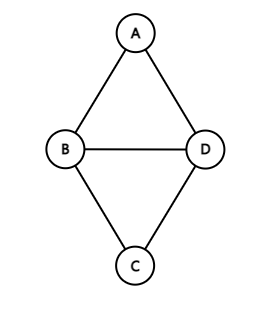
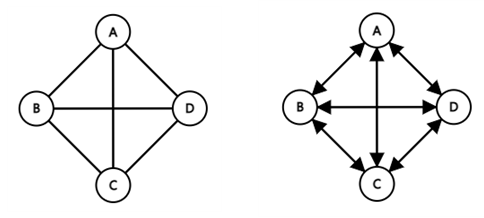
1. 무방향 그래프(Undirected Graph)

• 두 정점을 연결하는 간선에 방향이 없는 그래프

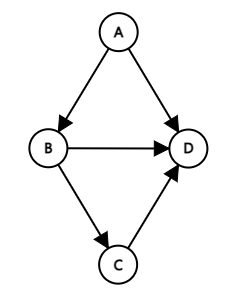
2. 방향 그래프(Directed Graph)

• 간선에 방향이 있는 그래프

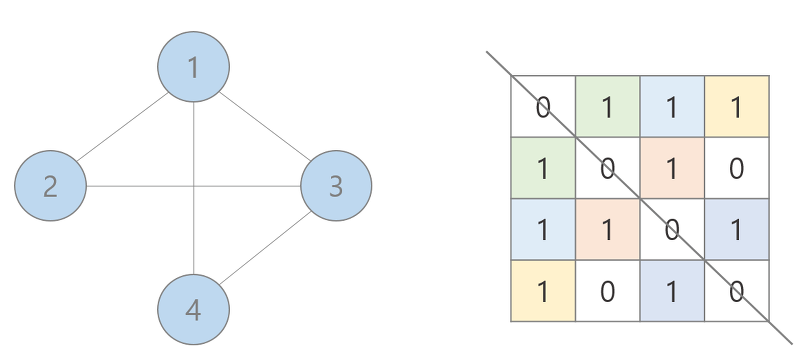
완전 그래프(Complete Graph)

• 한 정점에서 다른 모든 정점과 연결되어 최대 간선 수를 갖는 그래프

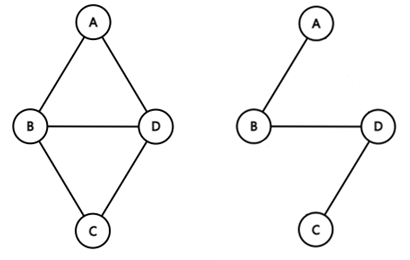
3. 부분 그래프(Sub Graph)

• 기존의 그래프에서 일부 정점이나 간선을 제외하여 만든 그래프

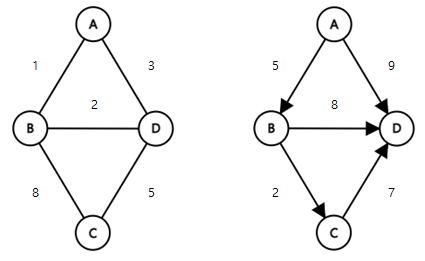
4. 가중 그래프(Weight Graph)

• 정점을 연결하는 간선에 가중치를 할당한 그래프

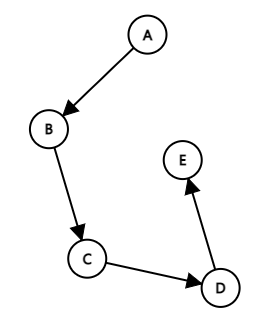
5. 유향 비순환 그래프(DAG, Directed Acyclic Graph)

• 방향 그래프에서 사이클이 없는 그래프

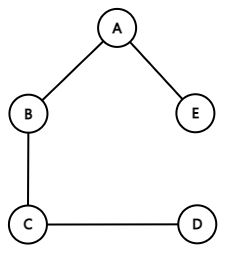
6. 연결 그래프(Connected Graph)

• 떨어져 있는 정점이 없이 연결된 그래프

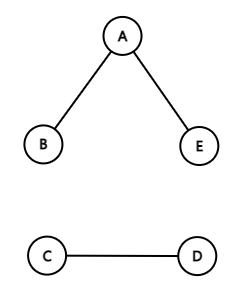
7. 단절 그래프(Disconnected Graph)

• 연결되지 않은 정점이 있는 그래프

그래프의 구현

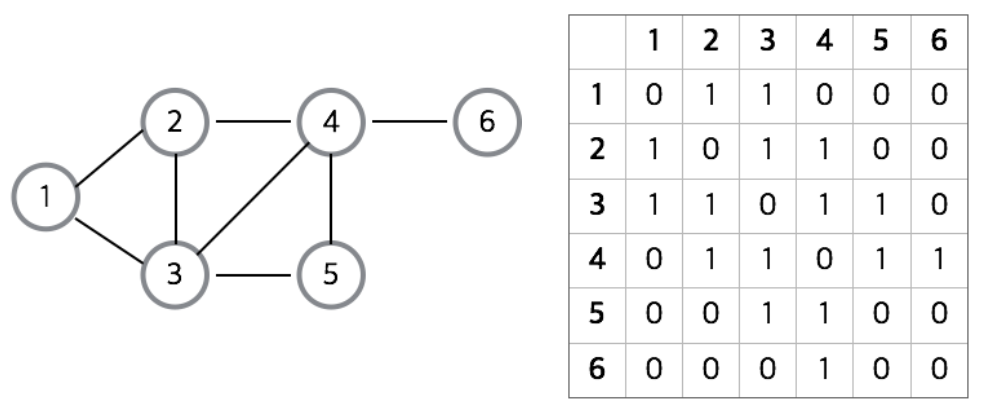
1. 인접 행렬(Adjacency Matrix)

• 그래프의 연결 관계를 이차원 배열로 나타내는 방식
• adj[i][j] : 노드 i에서 노드 j로 가는 간선이 있으면 1, 아니면 0

• 대각 성분을 기준으로 대칭인 성질을 가짐

장점

• 쉬운 구현
• 노드 i와 노드 j가 연결되어 있는지 확인하기 위해 adj[i][j]가 1인지 0인지 확인하면 되므로 탐색 시 O(1)의 시간 복잡도를 가짐
• 간선 삽입 및 삭제 시에도 O(1)의 시간 복잡도를 가짐

단점

• 모든 노드 쌍에 대한 간선 정보를 확인하려면 ⇒ 모든 가능한 노드 쌍에 대해 행렬을 조회해야 하기 때문에 O(V^2)

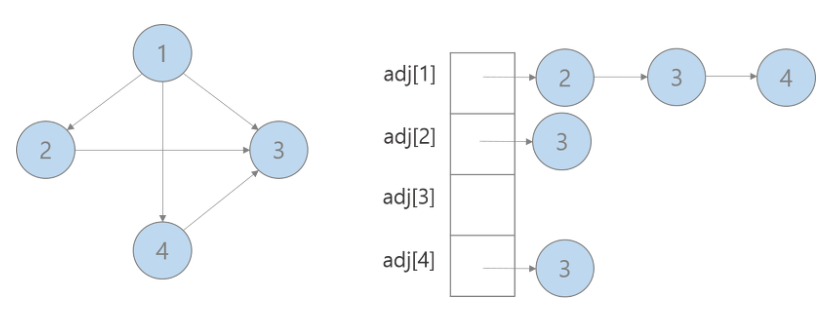
2. 인접 리스트(Adjacency List)

• 그래프의 연결 관계를 vector의 배열로 나타내는 방식
• adj[i] : 노드 i에 연결된 노드들을 원소로 갖는 vector

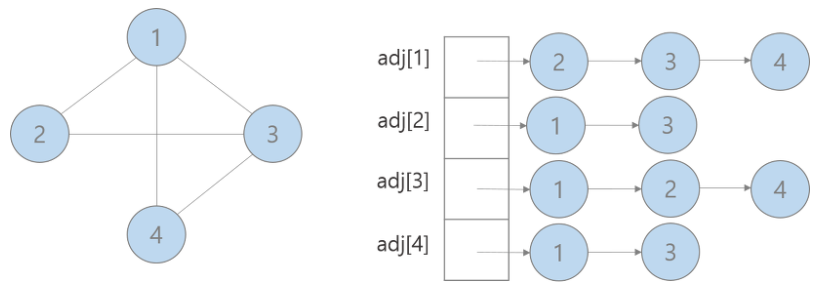
• 간선에 방향이 없는 무방향 그래프의 경우

장점

• 실제 연결된 노드들에 대한 정보만 저장 ⇒ 간선의 개수에 비례하는 리소스만 차지
• 노드에 대한 탐색 수행시 간선의 개수만큼의 시간이 걸림 O(E)
  • 각 노드에 연결된 모든 노드들을 방문해야 하는 경우 인접 리스트로 구현하는 것이 큰 이점을 가짐

단점

• 노드 i가 노드 j와 연결되어 있는지 확인하고 싶은 경우 ⇒ ad[i]의 vector전체를 돌며 j를 성분으로 갖는지 확인
  • 이 경우 시간복잡도는 O(V)가 될텐데 인접 행렬의 경우 adj[i][j]가 1인지 0인지만 확인하면 되므로 O(1)

Reference

https://velog.io/@humblechoi/자료구조-그래프

https://leejinseop.tistory.com/43

https://sarah950716.tistory.com/12