[Interview] Heap

힙

힙(Heap)란?

• 완전 이진 트리의 일종, 우선순위 큐를 위해 만들어진 자료구조
• 여러 개의 값들 중에서 최대값이나 최소값을 빠르게 찾아낼 수 있는 자료구조
• 루트 노드에 우선순위가 가장 높은(낮은) 데이터를 위치시킬 수 있기 때문에 우선순위 큐를 구현할 수 있는 자료구조

힙의 종류

• 최대 힙(max heap)
  • 루트 노드의 값이 가장 큰 경우
• 최소 힙(min heap)
  • 루트 노드의 값이 가장 작은 경우

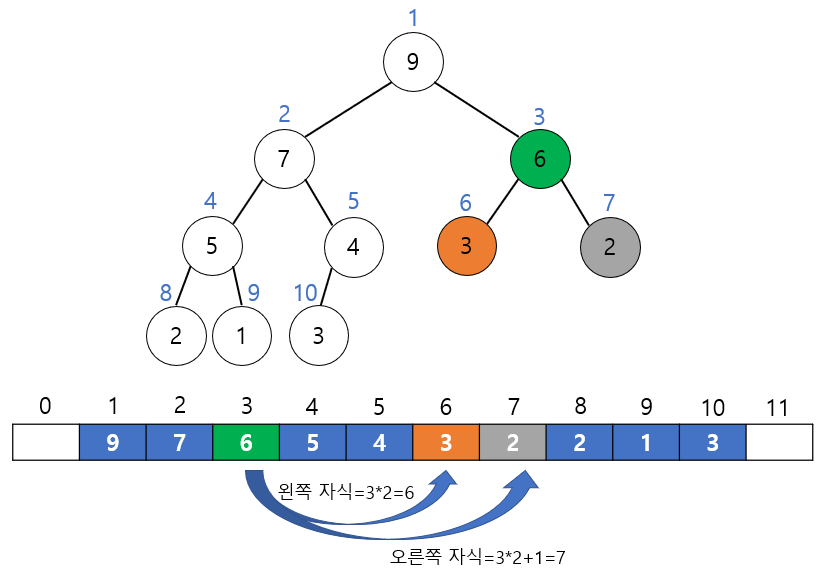
배열로 힙을 구현한 경우

• 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2
• 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 1
• 부모 노드의 인덱스 = 자식 노드의 인덱스 / 2

힙의 삽입

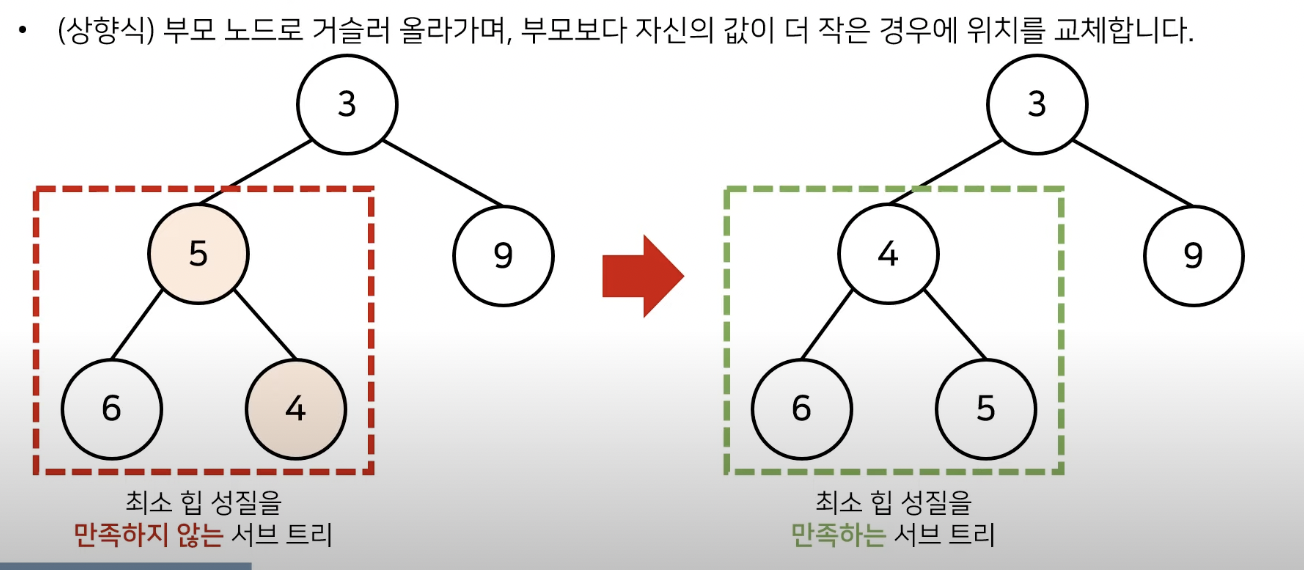
최소힙의 경우

• 새로운 원소를 힙의 가장 아래에 추가
• 추가한 원소를 부모와 비교
• 만약 부모보다 작다면 위치를 교환
• 계속해서 부모와 비교해서 부모보다 클 때까지 교환을 반복

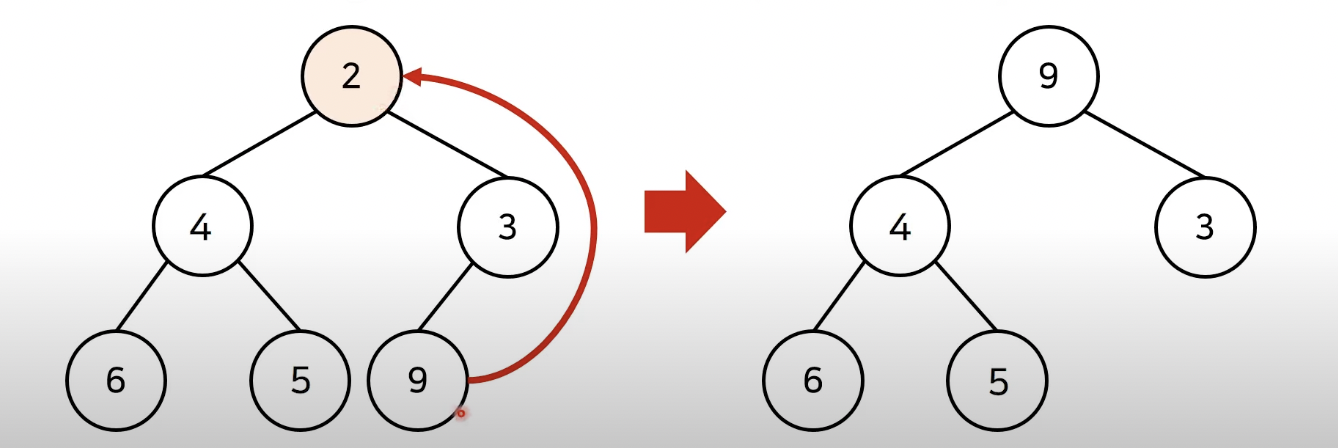
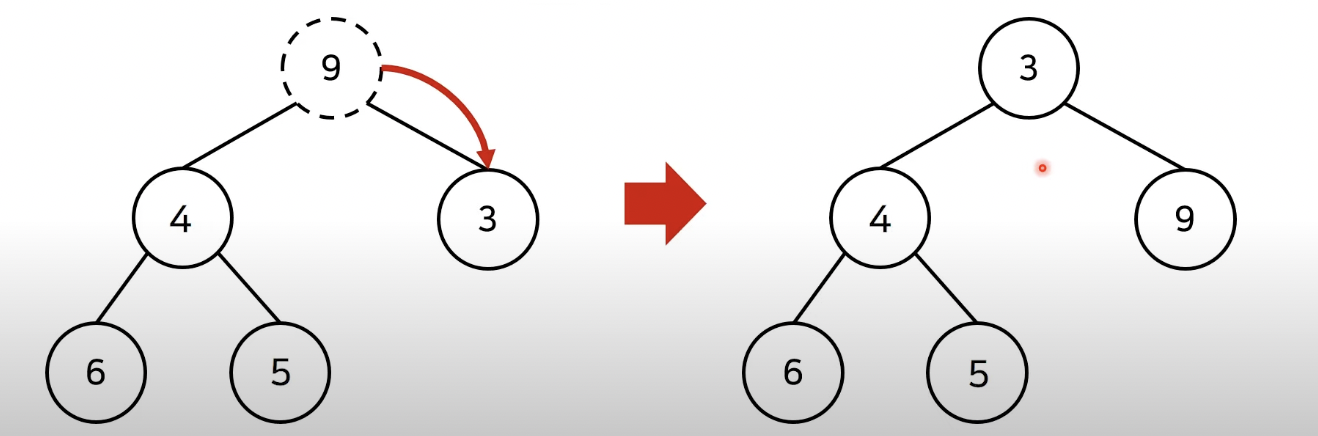
힙의 삭제

• 루트 노드를 삭제하게 될텐데 이 때 가장 마지막 노드를 대체시킴
• 그리고 힙의 성질을 만족하기 위한 연산을 수행

시간 복잡도

O(1)

• 최소, 최대값의 탐색

O(log n)

• 삽입, 삭제
  • 힙의 특성을 유지해야 하기 때문

Reference
https://velog.io/@yyj8771/자료구조-우선순위-큐Priority-Queue와-힙Heap

https://velog.io/@yun8565/우선순위-큐-Priority-Queue

https://velog.io/@yyj8771/자료구조-우선순위-큐Priority-Queue와-힙Heap

https://velog.io/@humblechoi/자료구조-트리와-힙