[Interview] Tree

트리(Tree)란?

• 정점(node)과 간선(edge)을 이용해 사이클이 이루어지지 않도록 구성한 그래프의 형태
• 계층적 관계를 표현
• 비선형 자료구조

• 정점이 n개인 트리는 항상 n-1개의 간선을 가짐

  

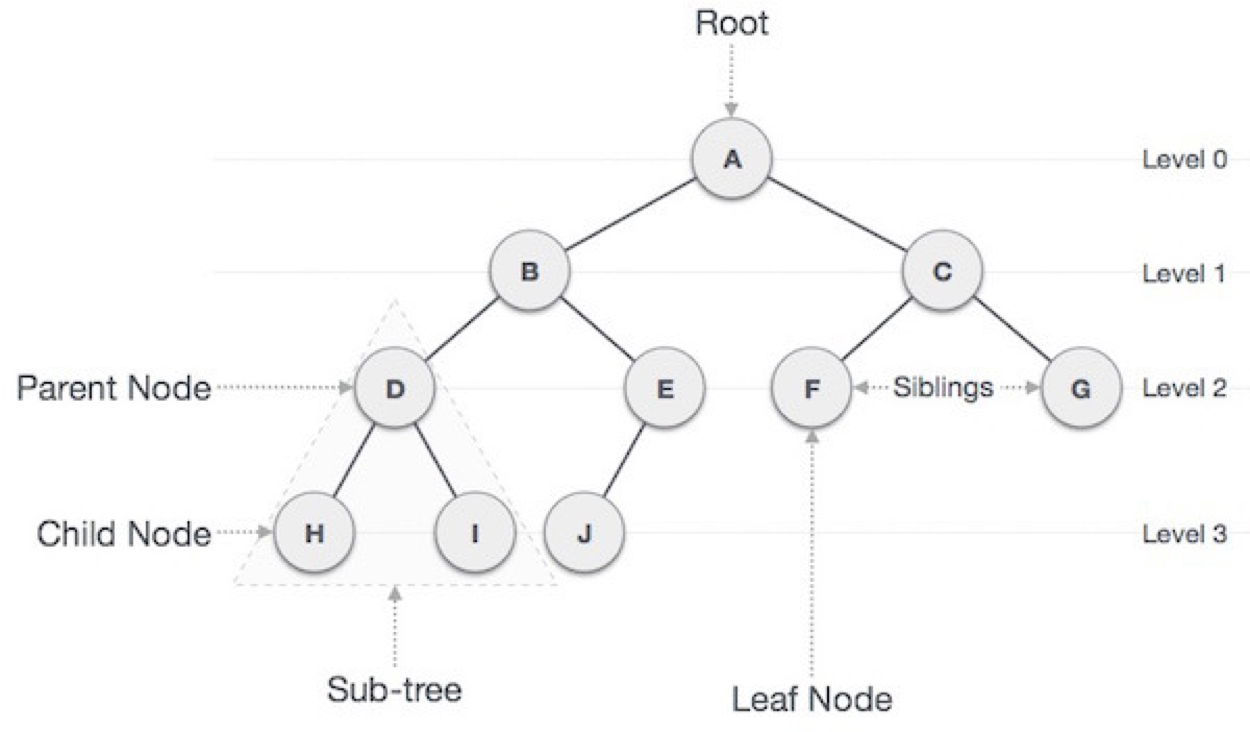
트리 관련 용어

• 노드(node)
  • 트리의 기본 요소로 데이터를 저장하는 단위, 각 노드는 한개 이상의 자식 노드와 연결되어 있다.
• 루트 노드(root node)
  • 트리 구조에서 최상위에 있는 노드, 모든 다른 노드들은 루트 노드를 통해 연결됨
• 자식 노드(child node), 부모 노드(parent node), 형제 노드(sibling node)
  • 노드 간의 관계를 부모, 자식 형제 관계로 표현, 노드의 관계는 상대적(부모 노드이면서 동시에 자식노드일 수 있음)
• 리프 노드(leaf node)
  • 자식 노드가 없는 노드
• 서브 트리(sub tree)
  • 트리 내에서 특정 노드와 그 자손 노드들로 이루어진 트리
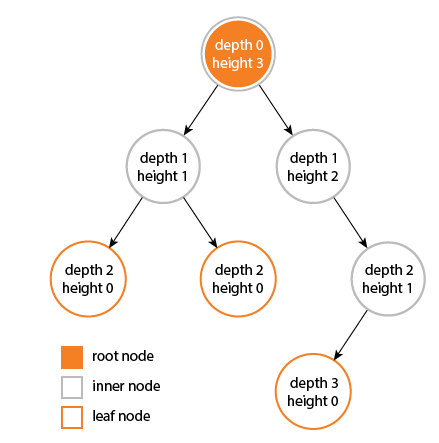
• 높이(height)
  • 트리의 높이는 루트 노드에서 가장 깊숙한 리프 노드까지의 최장 경로의 길이, 트리의 높이는 트리의 성능과 메모리 사용에 영향을 미침
• 차수(degree)
  • 어떤 노드의 차수는 해당 노드가 가지는 자식 노드의 수, 노드의 차수가 0인 경우는 리프 노드
• 깊이(depth)
  • 트리의 특정 노드로부터 리프 노드까지의 경로의 길이
• 레벨(level)

  • 트리의 각 층을 나타냄

    

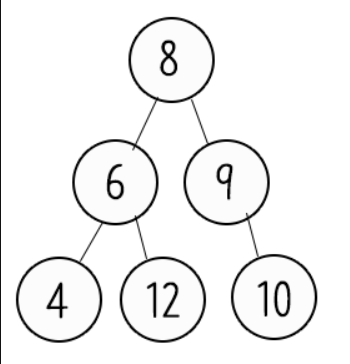
이진 트리(Binary Tree)

• 각 노드가 최대 두개의 자식 노드를 가지는 트리 구조
• 노드의 차수(degree)가 최대 2
• 이진 트리는 정렬되지 않은 데이터를 저장하고 효율적으로 탐색할 수 있는 구조를 제공

• 배열이나 연결 리스트를 기반으로 트리를 만들곤 함(각각 장단점이 있음)

  

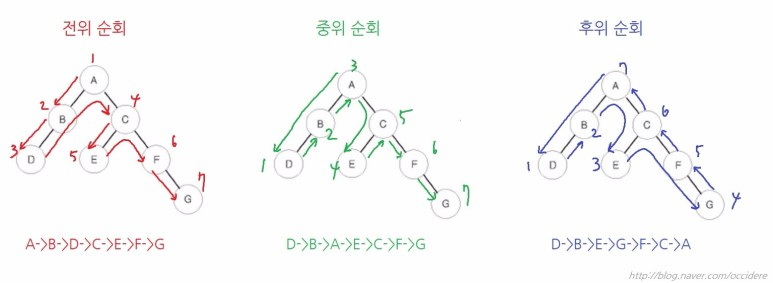
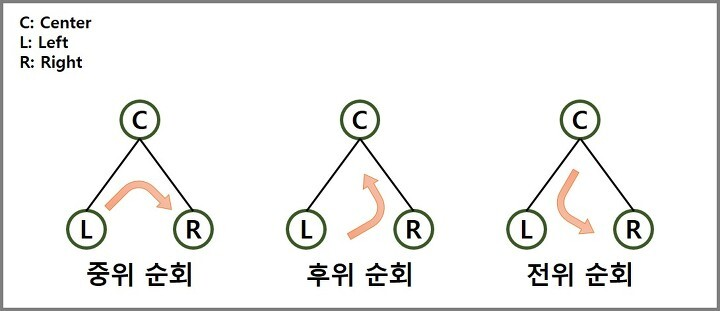
이진 트리의 순회

• DFS 순회
• 중위 순회를 이용하면 정렬된 원소의 목록을 획득 가능

시간 복잡도

O(1)

• 삽입, 삭제

O(n)

• 탐색: 최악의 경우 모든 노드를 순회

O(log n)

• 탐색: 트리가 균형을 유지할 경우

이진 트리의 경우 최선우 경우 트리를 탐색하고 삽입과 삭제를 하는데 O(log n)

최악의 경우 O(n)

이진 탐색 트리(Binary Search Tree - BST)

• 모든 부모 노드들의 left child는 부모 노드의 데이터보다 값이 작아야 함
• 모든 부모 노드들의 right child는 부모 노드의 데이터 보다 값이 커야 함

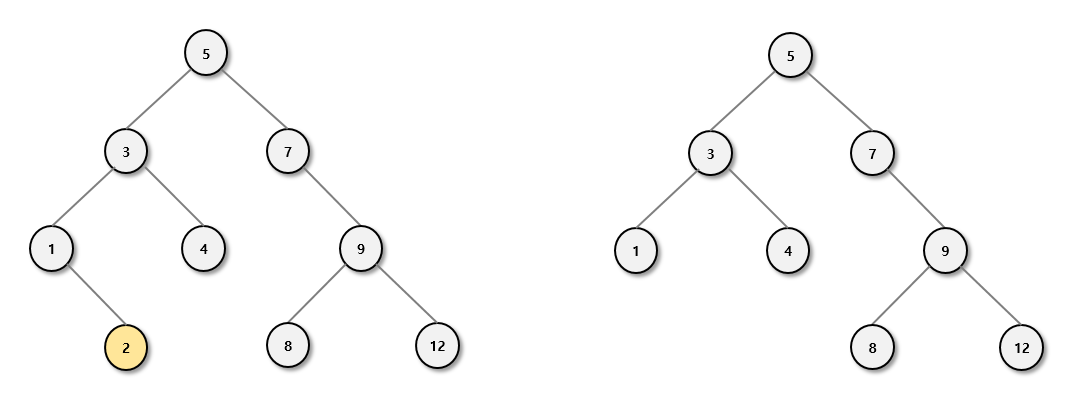
이진 탐색 트리의 삭제

• 삭제해야할 노드가 리프 노드인 경우
  • 삭제할 노드 2만 삭제하면 됨

• 삭제할 노드의 자식 노드가 1개인 경우
  • 이 경우도 규칙을 깨지 않고 7만 삭제할 수 있음

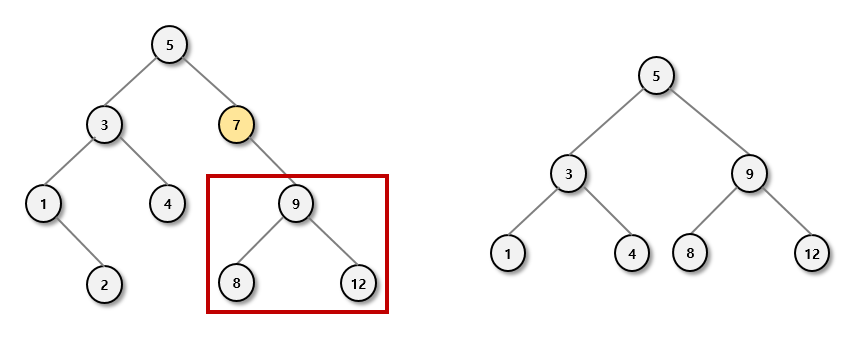
• 삭제할 노드의 자식 노드가 2개인 경우
  • 삭제할 노드의 왼쪽 서브트리에서 최대 값 노드
  • 삭제할 노드의 오른쪽 서브트리에서 최소 값 노드

시간 복잡도

O(n)

• 트리가 균형이 깨진 탐색, 삽입, 삭제

O(log n)

• 균형있게 유지된 트리의 탐색, 삽입 삭제

어떤 자료구조를 선택해야할까?

• 만약 트리가 주로 검색이나 정렬된 데이터를 다루는 경우에는 이진 탐색 트리가 적합, 탐색 연산이 O(log n)으로 빠르기 때문
• 그러나 데이터의 삽입, 삭제가 자주 일어나고 트리의 구조가 동적으로 변경되는 경우에는 균형을 유지하는 특별한 형태의 이진 탐색 트리(예: AVL 트리, 레드-블랙 트리)를 고려
• 이진 트리는 특별한 순서나 정렬이 필요 없는 경우에 사용

Reference
https://velog.io/@humblechoi/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC%EC%99%80-%ED%9E%99 https://velog.io/@yyj8771/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-Tree https://shutcoding.tistory.com/entry/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-Tree%EB%9E%80 https://mommoo.tistory.com/101 https://blog.naver.com/occidere/220899936160